
Уважаемые посетители нашего блога и сообщества Вконтакте! В рамках новой рубрики «Люди, открытия, изобретения» мы представляем вам следующую книгу из редкого фонда читального зала.
Это труд Исаака Ньютона «Математические работы», напечатанный в серии «Классики естествознания» в 1937 г.

Перевод с латинского, вводная статья и комментарии Д.Д. Мордухай-Болтовского. Переводчик отмечает, что «настоящий перевод Ньютона сделан с латинского издания Кастильона и снабжен обширными комментариями. Я нашел также излишним помещать все письма Ньютона и выбрал только те из них, которые непосредственно относятся к математике и по своей конструкции приближаются к типу научной статьи».
Наиболее значительной из помещенных в книге работ Ньютона является «Метод флюксий».

Работа была написана в промежутке 1664-1671 гг., часть ее содержания входит в книги, опубликованные уже во время Ньютона, однако сама работа была опубликована только после его смерти (1736). Ньютон, прекрасно владея латынью, пишет «Метод флюксий» на латинском языке. Именно на этом языке, существовала, хорошая, вполне фиксированная математическая терминология. Затем рукопись Ньютона попала в руки Кользону, который недостаточно хорошо владел латынью, решил издать ценную работу Ньютона со своими большими комментариями.

Кользон освободил себя от трудной работы перевода этих комментариев с английского на латинский и перевел книгу на английский язык. Следующий издатель «Метода флюксий» уже располагал не латинской рукописью Ньютона, а только английским переводом. Бюффон сделал перевод на французский язык не с латинского, а с английского языка. Кастильон перевел ее опять с английского на латинский. Этот «исправленный» латинский перевод и был взят для перевода на русский язык Д.Д.Мордухай-Болтовским, именно «вследствие указанной выше большей определенности и фиксированности латинской математической терминологии».
Английский учёный Исаак Ньютон внёс неоценимый вклад в естествознание и прославился в истории как выдающийся физик, совершивший множество открытий, существенно повлиявших на ход развития науки.

Помимо этого, Ньютон интересовался математикой, механикой и астрономией. Сегодня открытые Исааком Ньютоном законы до сих пор остаются актуальными и в обязательном порядке изучаются в рамках школьного курса физики.
Исаак Ньютон прожил долгую и насыщенную жизнь. Его жизненный путь начался 25 декабря 1642 года, когда он появился на свет в деревне Вулсторп, затерянной на просторах графства Линкольншир в восточной части Англии. Его отец, землевладелец, на тот момент был мёртв и все обязанности по воспитанию мальчика легли на плечи состоятельной матери.

В детстве Ньютон отличается замкнутостью и имел мрачный характер. Любимым занятиями Ньютона в этом возрасте являлось чтение литературы, но также он не упускал возможность сконструировать что-то примитивное из подручных материалов. Однажды он наполнил надувной шар горячим воздухом и испытал это средство воздухоплавания, посадив вместо пилота своего кота. Ни шар, ни кота никто больше не видел.
В возрасте 12 лет мать отдала Ньютона в Грэнтемскую школу.

Изначально он был посредственным учеником, но после избиения более сильным сверстником получил моральную травму, которая привела к резкой активизации умственных усилий и желанию выбиться в лучшие ученики. Природные способности Ньютона поспособствовали этому,и уже скоро он стал лучшим учеником, на что обратили внимание педагоги. В 1659 году Ньютону пришлось вернуться домой для занятия фермерством, так как матери требовалась помощь.
В 1661 году Исаак Ньютон поступил в Кембриджский университет, где успешно занимался различными науками за исключением геометрии.

Студентом он не производил впечатления будущего светила науки. В 1663 году после прослушивания лекций профессора Барроу у Ньютона возник повышенный интерес к математике и он даже открыл собственный метод. Позже, когда в 1665 г. великая эпидемия чумы опустошила Лондон и окрестности, студентов поспешно разослали по домам, пока мор не дошел до Кембриджа. Вернувшись на родительскую ферму, Ньютон стал серьезнее относиться к науке в целом и в частности к математике. Он успешно окончил университет, получив степень бакалавра. В возрасте 26 ему предложили работать профессоров математики, на что он охотно согласился. Это стало его основной профессией на долгие 27 лет и открывало простор для научных изысканий. Именно тогда Ньютон смог совершить свои открытия, которые в дальнейшем сыграли огромную роль в науке.
В 1689 года Ньютона пригласили в парламент, который сверг Стюартов. Политика не пришлась по вкусу Ньютону, и уже через год он возглавил лондонский монетный двор, пробыв в этом статусе целых 32 года. Последние годы для учёного были счастливыми, ведь он имел стабильный и большой доход, пользовался уважением в обществе и в его окружении находилось большое количество образованных людей и учёных, которые прислушивались к Ньютону и вдохновлялись на совершение собственных научных изысканий.
Посвятив свою жизнь науке, Ньютон так и не вступил в брак. Хозяйственными делами в Лондоне занималась племянница. Умер выдающийся учёный 20 марта 1727 года, но его имя и труды всё ещё живут в физической и математической науках.
В 1665–1666 гг. он вывел свой закон тяготения, объясняющий движение планет, развил законы механики, чтобы проанализировать движения любого рода для всех физических тел, изобрел дифференциальное и интегральное исчисления, совершил важные открытия в оптике.

Что характерно, он не спешил публиковать свои труды, но как ни в чем не бывало вернулся в колледж, получил степень магистра и стал членом Тринити-колледжа. Затем его избрали на должность Лукасовского профессора математики, а в 1669 г. подал в отставку предыдущий профессор, Барроу. Ньютон не прославился как преподаватель, на его лекциях было мало студентов.
Подход Ньютона к вычислению производных в основном напоминает подход Лейбница, только вместо dx он использовал o, а значит, его метод грешил той же логической проблемой: он давал приблизительный результат. Однако Ньютону удалось показать: если принять о за бесконечно малую величину, приближение станет намного точнее. И когда мы дойдем до предела, где o станет такой малой, какой нам угодно, ошибка исчезнет. Поэтому Ньютон утверждал, что его результат точен. Он изобрел новое слово «флюксия», чтобы подчеркнуть главную идею: величина стремится к 0, но никогда не достигает его.
В 1671 г. он создал более обширный труд, «Метод флюксий и бесконечных рядов».

Первая книга, посвященная исчислению, так и не была опубликована вплоть до 1711 г., вторая увидела свет в 1736 г. Однако несомненно, что уже к 1671 г. Ньютон оперировал всеми основополагающими идеями исчисления.
Сановный противник этого метода епископ Джордж Беркли в 1734 г. в своей книге «Аналитик, или Рассуждение, адресованное неверующему математику» указывал, что это противоречит логике: делить числитель и знаменатель на о, если впоследствии о будет равно 0. В итоге вся процедура сводится к тому, что дробь на самом деле выглядит как 0/0, а это, как всем известно, полная бессмыслица. Ньютон возражал, что он не уменьшает о до нуля, он исследует результаты того, что она сколь угодно близко подходит к 0, не становясь ему равной, и вообще его метод исследует флюксии, а не числа.
Математики пытались найти выход в аналогиях с физикой: Лейбниц прибегал к определениям «дух утонченности» и противоположному ему «дух логики», но по сути Беркли был прав. Ученым потребовался век, чтобы обнаружить убедительные ответы на его возражения, найдя для интуитивно открытого «приближения к пределу» строгое определение. Тогда-то исчисление преобразилось в более искусную науку – математический анализ. Но на протяжении этих 100 лет никого, кроме Беркли, так и не обеспокоили логические изъяны, и исчисление развивалось невзирая на них.
Метод процветал, потому что Ньютон был прав, но лишь через 200 лет его интуитивная концепция флюксий была сформулирована с безупречной логикой, в терминах пределов. К счастью для математиков, задержка с этим открытием не застопорила процесс развития науки в целом. Исчисление оказалось слишком востребованным и важным методом, чтобы отказаться от него из-за нескольких логических софизмов. Беркли в негодовании утверждал, что метод только кажется действенным, поскольку в нем различные ошибки взаимно компенсируют друг друга. Он был прав – однако понятия не имел о том, почему ошибки компенсируют друг друга. Ведь если это правда – то это и не ошибки вовсе!
Ньютон очень плохо переносил критику и когда в 1672 г. издал свои исследования природы света, то услышал много нелестного о своей работе, что надолго отбило у него охоту предавать огласке свои открытия. Но эпизодически он всё же отваживался издавать некоторые работы и даже написал две книги. А для себя Ньютон продолжал развивать свои идеи о тяготении, и в 1684 г. Галлей снова попытался уговорить его опубликовать эти труды. Но для этого, помимо страха перед критикой, существовало и техническое препятствие. В своих рассуждениях ученый был вынужден объявить планеты точечными частицами с массой, не равной 0, но нулевыми размерами, что не соответствовало действительности и заведомо привлекло бы к нему нежелательное внимание критиков. Он хотел бы заменить эти невероятные точки на сферические тела, но не мог доказать, что силы взаимного тяготения между сферами такие же, как и между предельно малыми точками с равной массой.
Только в 1686 г. Ньютону удалось заполнить этот пробел, и в 1687 г. свет увидели «Математические начала натуральной философии».

Они содержали множество свежих идей. Самыми важными стали математические формулы законов движения, расширяющие работы Галилея, и тяготения, основанные на законах Кеплера.
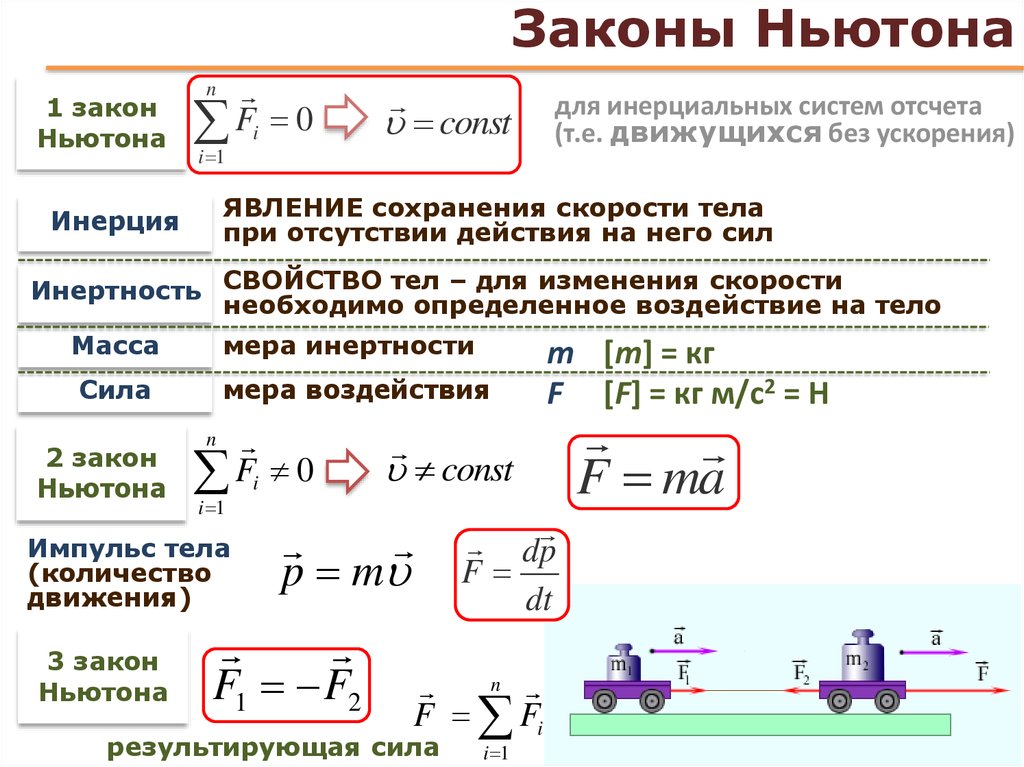
Главный закон движения по Ньютону (есть и дочерние, следующие из него) утверждал, что сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Иными словами, скорость является производной от положения тела, а ускорение – производная от скорости.
Закон тяготения утверждает, что все материальные частицы притягиваются друг к другу с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними. Так, сила тяготения между Землей и Луной станет сильнее в четыре раза, если Луна будет ближе к Земле в два раза, или в девять, если расстояние уменьшится втрое. И снова, поскольку речь идет о воздействии силы, здесь имеется вторая производная.
Ньютон вывел свой закон из трех законов Кеплера о движении планет. Опубликованный им труд стал высшим достижением классической евклидовой геометрии. Ньютон сознательно избрал этот способ подачи материала, поскольку тот был основан на знакомых математических понятиях, а значит, менее уязвим для критиков. И всё же многие аспекты «Начал» появились на свет исключительно благодаря неопубликованным методам исчисления, открытым Ньютоном.
«10 фактов из жизни Исаака Ньютона». Ресурс свободного доступа.
«УЧЕНЫЕ МУЖИ БОЖЬИ. ИСААК НЬЮТОН». РЕСУРС СВОБОДНОГО ДОСТУПА.
Мы много раз слышали: «наука не оставляет места для Бога, она несовместима с верой. Занятие научной деятельностью открывает ученым глаза, и они становятся атеистами». Это — беззастенчивая ложь. Современная наука заложена людьми, искренне верившими в Бога. Более того: они постоянно утверждали, что именно вера в разумность и совершенство Божьего замысла, воплощенного в мироздании, подвигла их на постижение и понимание законов, заложенных во Вселенную ее Создателем. Эта серия видео роликов содержит информацию об ученых мужах, которые являются светочами веры в дивные дела Божьи — во всемогущество, совершенство и милость Творца. Она адресована учащимся, учителям, а так же всем, кто интересуется историей науки и вопросом совместимости веры и знания.
Спасибо, что были с нами! До скорой встречи на нашем блоге!
